加试考4道题，代数、平面几何、数论、组合各一道。其中的第二题为几何题，此文记录本人对此题的思考和探究、解答过程。

题目如下：

在凸四边形ABCD中，AC平分∠BAD,点E、F分别在BC、DC上，满足EF//BD,

分别延长FA,EA至点P,Q，使得过点ABP的圆及ADQ的圆均与AC相切。

证明：B,P,Q,D四点共圆。

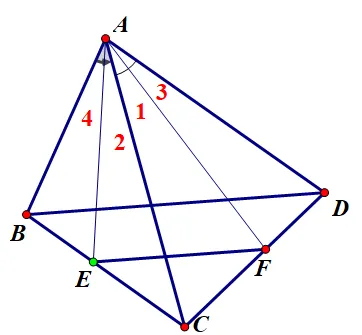
第一步，根据题意画出准确的图形，

题目中的条件几何意义明显，都容易作出来，按部就班画图即可，

得到的准确图形如下。

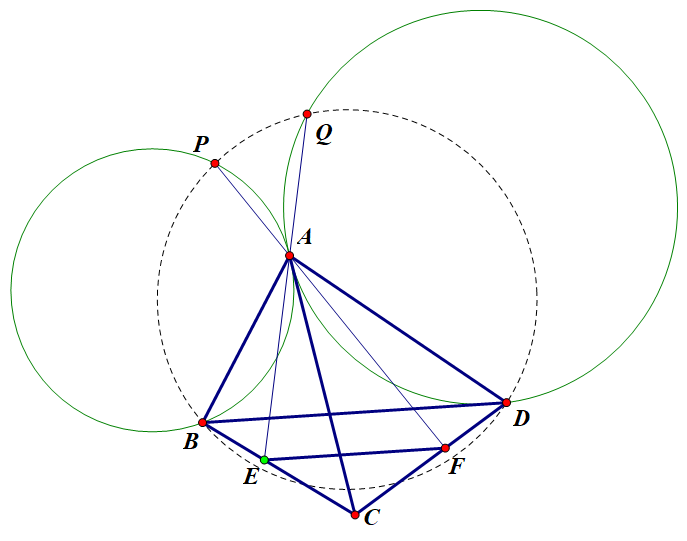
第二步，挖掘结构的基本性质，

由角平分线及相切得∠BPA=∠BAC=∠DAC=∠DQA,

由EF//BD得BE/EC=DF/FC,

第三步，从结果入手，

证明四点共圆的常用方法主要有四个：

1、倒角，2、倒比例，3、找圆心，4、托勒密。

先尝试倒角，希望不大，主要是角度都不好刻画，也无法传递。

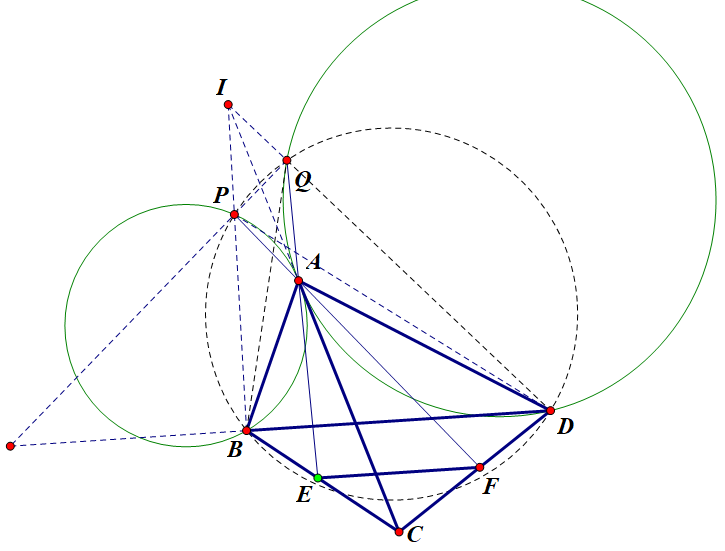
再尝试倒比例，直线BQ,DP似乎都不好，没有好的性质。

BD直线很好，但是PQ不好，其交点也没发现什么性质。

BP,DQ还行，其交点I应该在AC上，因为这样利用切割线定理

即得IP*IB=IA^2=IQ*ID,从而证明结果。

这条路感觉靠谱。

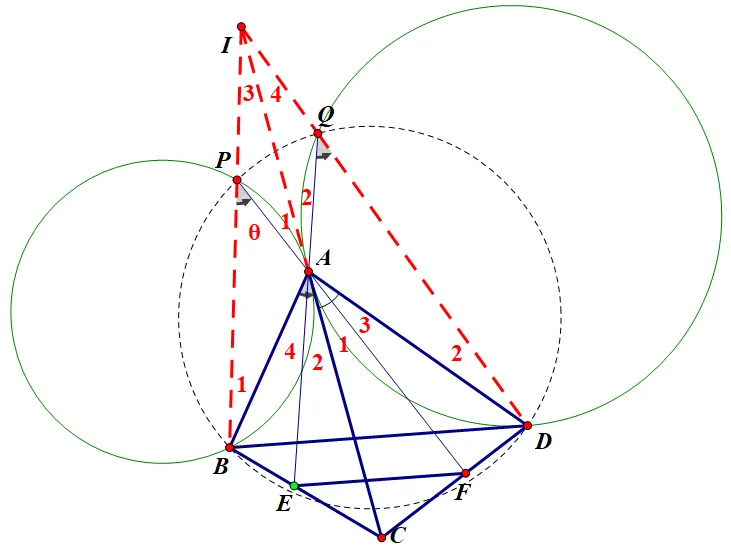
第四步，适当转化问题，尝试消点。

删除上图中的冗余元素，下面考虑在下图中如何证明三线共点。

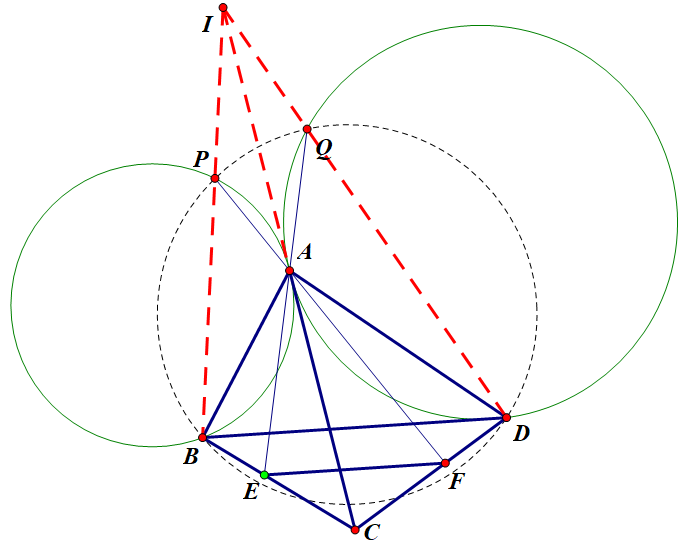
CA显然非常好，可以设BP交CA于I，只要能刻画出I即可。

最自然的想法是算出IA，考虑到条件中很多角度关系，

最好的选择是正弦定理。

为了方便书写，可以设出四个小角，

从而得到其余角如图所示，

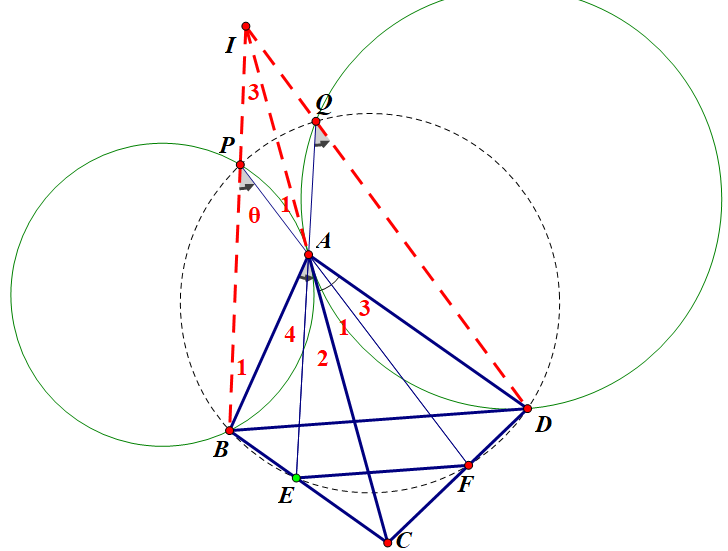
在△IPA中,AI=AP*sinθ/sin∠3,

在△BPA中,AP=AB*sin∠1/sinθ,

故AI=AB*sin∠1/sin∠3,

同理AI'=AD*sin∠2/sin∠4,

从而只需证明AB*sin∠1/sin∠3=AD*sin∠2/sin∠4,

这样就能消去I,P,Q和两个圆。

得到下图。

在此图中上述结论基本是显然的，利用分角定理及

平行线分线段成比例定理计算即得。

第五步，适当简化整理证明，

上述证明中，欲算AI，可以直接在△IAB中，故可以再简化，

最后证明整理如下：

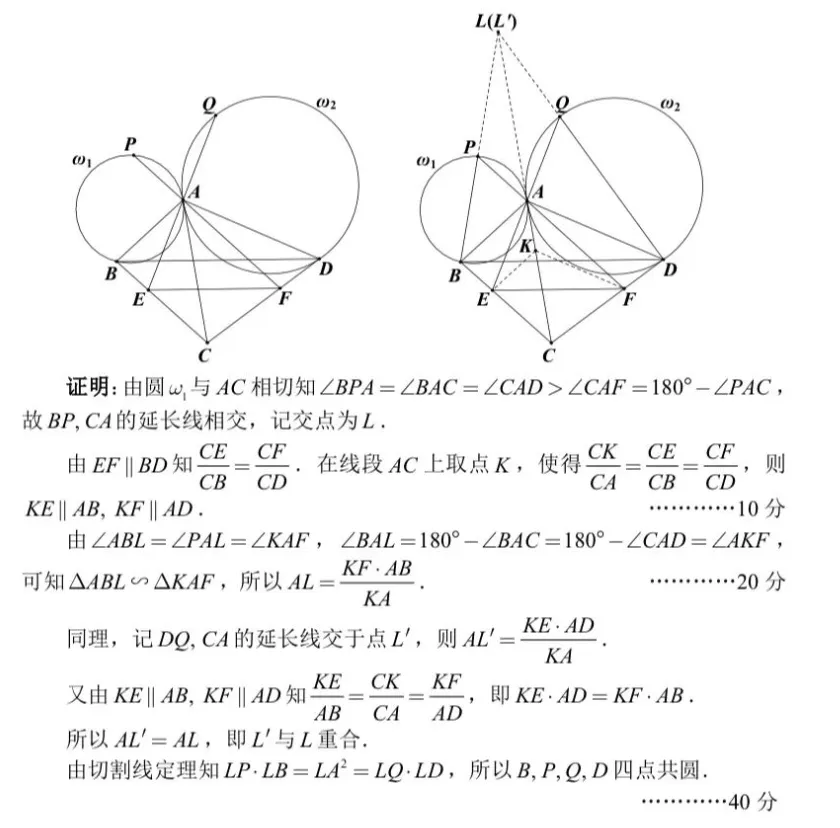
证明：

如图，设BP,DQ交CA于I,I'，∠BAD内四个小角为∠1,∠2,∠3,∠4,

则θ=∠1+∠3=∠2+∠4=∠BPA,

故∠PIA=θ-∠1=∠3,∠PBA=∠PAI=∠1,

由EF//BD得BE/EC=DF/FC,

即AB*sin∠4/(AC*sin∠2)=AD*sin∠3/(AC*sin∠1),

即AB*sin∠1/sin∠3=AD*sin∠2/sin∠4。

△ABI中,由正弦定理得AI=AB*sin∠1/sin∠3,

同理AI'=AD*sin∠2/sin∠4,

∴AI=AI',即I,I'重合。

则IP*IB=IA^2=IQ*ID,

即PBDQ四点共圆。

最后对上述解法做一总结归纳，并简单点评试题。

上述解答的关键是从结果倒推，发现四点共圆等价于三线共点，进而利用正弦定理将结果转化为ABCD中的基本量，最后简单三角计算即得。当然本题还有很多其他的思路和解法，基本都是可以通过正弦定理计算来证明。

官方提供的参考答案如下，前面思路和我类似，都是将结果转化为三线共点。他没用使用三角计算，是通过几何方法，使用作平行线和相似三角形来得到的，十分精妙。但是不易想到，估计采用参考答案的解法的学生不多。

   平心而论，本题难度不算高，入手角度也不少，计算也比较自然。我的上述解答中，没有用到太多的几何性质和方法(相似,共圆)，相对前几年的几何题目，感觉此题难度算是比较低的。题目的风格与前几年的题目也有所不同。前几年的题目几乎都必须要多次使用共圆、相似等几何性质和技巧，对几何能力（寻找共圆、相似）的要求较高，而本题只要按图索骥，从结果分析，将结果适当转化为恒等式，稍加计算即可完成。要求较高的分析问题的能力，而对几何能力要求有所降低。

转自微信订阅号：金磊几何

本人对本题的以上解法主要用到了消点法和简单的圆幂知识，对这两个知识感兴趣的读者可以参考拙著《圆幂与根轴》。