|
van’t Hoff 是以渗透压和化学动力学的研究成果而获第一位诺贝尔化学奖的世界著名科学家,一百多年来,人们一直用写在世界各国物理化学教科书中的范氏渗透压公式 来解释渗透过程。根据范氏定律,渗透压与溶液的浓度和温度成正比,它的比例常数就是气体状态方程式中的常数 R,并据此导出了范氏渗透压公式。不过,范氏渗透压公式只能近似用于理想稀溶液,而随着溶液浓度的渐渐增大,计算值就会越来越偏离实际值,这就导致用范氏渗透压公式来解释渗透过程,仍有很多难以自圆其说之处。之所以如此,是因为客观上还存在一个能从本质上解释渗透过程的科学概念尚未被我们抽象出来。
宏观的化学热力学认为:渗透现象是溶液中溶剂的化学势与纯溶剂的化学势差造成的,并可以用经验定律—Raoult's law 导出渗透压方程,但人们并不清楚这种化学势差推动渗透现象的微观过程。在 1980 年代末,由美国物理学评述委员会组织的等离子体和流体物理学专门小组曾这样描述:迄今还没有一个可以接受的理论能解释渗透的微观结构。因此,他们将渗透现象的微观结构列为 1990 年代的物理学重要课题之一。但直到现在,仍没有取得实质性的进展。
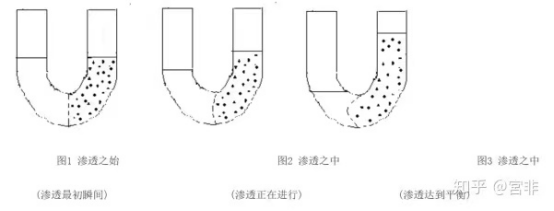
既然用范特霍夫渗透压公式之所以不能很好地解释渗透过程,其根本原因在于范氏的渗透压这个概念,不是从能充分暴露渗透全部本质的动态过程中抽象出来的,相反地,它是从为了阻止渗透过程进行一静态中测出来的 (其值就是为了阻止渗透过程进行保持图 3 那样的状态,需要在溶液面所施加的力 ),这决定了它不能胜任对渗透这动态过程的解释。关于这一点,我们从范特霍夫定律或渗透压公式 可以看出,除了「摩尔气体常数,gas constant,gas-law constant,R」和一定条件下不变的「热力学温度,absolute temperature,T」外,渗透压只与摩尔量(quantity) 浓度一一对应,作为一个要描述渗透过程的概念渗透压,它没有涵盖到渗透过程的另一个必要的因素──压强 (膜上的压强),而且是渗透过程进行中变化着的压强,这样一来,范特霍夫渗透压公式不能胜任对渗透过程的解释也就不足为怪了。而渗透力这个概念却不同了,我们从渗透力公式 可清楚看出 (F 是渗透力;P 是膜上的压强;Ci 是溶质的摩尔量浓度;k 是平衡系数 (equilibrium constant)),渗透力同时涵盖了渗透过程进行两个必要而充分的因素──浓度和压强,所以以渗透力为核心概念的渗透定律能够胜任对渗透过程的解释。
所谓膜上的“压强”,不仅指膜上的液压,还应包括大气压。因膜两侧的大气压虽基本相同,但由于两侧的浓度不同,相同大气压对膜两侧所增加的渗透力是不同的(即大气压对膜两侧的「同量异效」性,浓度差越大「异效」越大。这也是有些教科书对植物体内渗透压之高 “让人感到意外” 的原因),所以膜两侧相同的大气压不能忽略或「对消」。而所谓「渗透有效膜面积」,速溶剂分子碰撞膜的面积。膜面积被溶剂和溶质分子共同碰撞触及,而只有被溶剂分子碰撞触及的面积才对渗透有效 (其他可称作「渗透无效膜面积」)。有效、无效两种膜面积的具体位置瞬息万变,但其比例对同一浓度的溶液来说是不变的;这两种膜面积的绝对值不易测定,但可以通过渗透平衡时膜两侧渗透力相等,而纯溶剂侧的渗透有效膜面积是 100% 而将溶液侧有效、无效两种膜面积都换算出来。
由于半透膜两边溶剂的浓度不相同,以致单位时间内由纯溶剂扩散进入溶液的溶剂分子数目,要比从溶液扩散进入纯溶剂的溶剂分子数多,从而导致了渗透现象的发生;并认为渗透压不是溶质分子的压力,而是溶剂扩散引起的。但是教科书上至今还不能用“扩散理论”定量地解释渗透压为什么可以用理想气体状态方程来计算这个问题。另一个问题是如果按照教科书的理论,当热水与冷水用半透膜隔开时,由于热水中水分子的扩散速率快,故热水应通过半透膜向冷水渗透。但迄今还没有人观察到这个现象,这说明教科书理论还值得怀疑,而渗透现象也可能是另外一种机制所致。
所以我们总结以上数据认为:渗透力同时涵盖了渗透过程进行两个必要而充分的因素──「浓度」和「压强」,所以以渗透力为核心概念的「渗透定律」能够胜任对渗透过程的解释。
|