在上一篇物种多样性维持机制的数学分析之后，这次趁热打铁，再续一篇。这回，我们来聊一聊共存物种能在多大程度上彼此相似，又能在多大程度上分化。换言之，物种的相似和分化是有极限的，我们可以从三个角度来理解：

第一：任一物种的数量有下限，这种下限就给物种丰富度有极限；

第二：任一物种数量有上限，这种上限给物种丰富度增加提供了更多的可能；

第三：环境的不稳定性为物种分化设置了上限，在一定的分化程度上，竞争会使得共存的物种之间的相似性有极限。

好，问题来了，怎么用数学去进行推导？

竞争限制了相似性

我们还是从Lotka-Volterra种间竞争模型先入手，不太了解这是啥的同学可以回顾一下物种多样性维持的机制的介绍。上一次我们介绍了两个物种或者是某一物种在一个群落里是如何竞争的，这次我们假设有三个物种，则这一模型我们可以写为：

（1）

（2）

（3）

角标1、2、3是代表的三个不同的物种，r是个体的平均生育率，N表示种群数量，K表示物种的环境容纳量，某些情况下也可以理解为适合度，α代表对某一种群的影响。比如代表物种1对物种1种群数量的影响（本物种对本物种的影响也可以取之为1），则代表物种2对物种1种群数量的影响，以此类推。

所以方程1，翻译成文字可以表述为：物种1种群数量随时间的变化等于个体的平均生殖率乘以种群数量再乘以种群自身和群落重其他种群对本种群的影响系数。

现在我们来对三个物种进行生态位分化，假设物种3的生态位在物种1和物种2的种间，并且与两个物种生态位的重叠幅度相等（举个例子，比如物种1生活在水下0米-200米的深度，物种3生活在水下100-300米的深度，则物种2的生活空间是水下50-250米）。

则，也就是说物种1和物种3对物种2的影响是等效的，，也就是说物种1和3之间的相互影响是相同的，如果二者没有生态位重叠或竞争关系，则值为0。此外，，也就是说物种1和物种3的适应性是相等的，如果没有生态位重叠，这个K也可以表示两个物种的环境容纳量。

如果物种2要能够在群落里生存下去，那么物种2在哪怕数量很小的时候也需要保持一定的增长率。那我们现在假设物种2数量很小，趋近于0，而物种1和物种3数量很大，那我们此时方程（2）任然需要大于0，即：；那物种1和物种3数量很大，趋近于各自的环境容纳量，而这个环境容纳量可以写为（两个物种的环境容纳量相等，以物种1为例，由于受到了物种3的营销β和自身的影响1，因此其环境容纳量不可能达到K，而是K除以自身和物种3对自己的影响。），因此此时，物种2需要存活下来的条件就可以写为：

(4)

同理，如果方程（4）左边小于了右边，则说明物种2最终会因为竞争排斥而消失在这个群落里。

那么如果，则方程（4）可容易成立，但同事也得考虑α和1+β的大小关系。那么现在我们来更进一步的讨论三者的关系。

听说你们很害怕微积分？

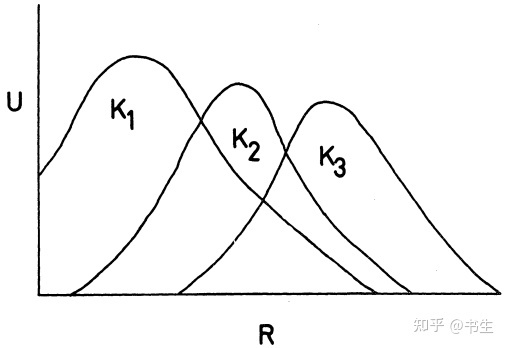
这里R代表的是某种资源，也可以理解为生态位宽度，U代表的是物种个体对该资源使用的概率，则三条曲线就是物种个体在这个生态位上的概率分布，那么每条曲线和R之间形成的面积，就是物种的数量。那么买面积要怎么求呢？积分。比如，我们把物种1的曲线定义为关于R的函数，即，则其积分就是曲线底下的面积，即：

(5)

这里，我们可以认为重叠部分的面积就是物种收到的种间竞争的影响。在经过了一系列的赋值和计算之后，大家发现无论怎么改变曲线的性状或设定三个物种在横轴上的重叠宽度，如果要某一物种成功进入这个新的生态系统，最后α的值都大概是略高于1/2（比如设置为复杂的以e为底的幂函数，之后算出来的条件为α>0.544，原文在这里给出了复杂的证明和计算过程），并且这个值独立于生态位的宽度。因此，如果某一物种所占据的生态位宽度有一个最小值，则一个资源均匀分布的环境中，物种的数量上限拒绝于这生态位的总宽度。

演化过程对相似性的限制

这里先夹带一点私货。个人认为把“evolution”翻译为演化更加准确，他指的是生物对环境的不断适应的过程。“进化”一次在生态学上有两个意思，作为动词的时候代表种群基因型频率的改变，作为形容词的时候，说某一物种更加进化只是代表这个物种在时间轴上出现的时间比较晚，而不代表它比那些古老的物种更成功。说的文一点，“evolution”是中性的，“演化”也是中性的，“进化”则多少有一点褒义。但是我明白，很多人已经习惯了说“进化”，所以本章的题目如果你觉得有点拗口，也可以把他理解为是“进化过程对相似性的限制”。

言归正传。之前我们讨论了物种所处得生态位和生态幅对共存的影响，那么生态位和生态幅是否会在种间作用中改变呢？

我们首先仅关注生态位。图2和图3左边的横轴表示物种的表型，P和Q定义为沿着某个环境梯度的生态位中点（比如叶片数量，个体大小等等），那他们考得越近，相似性越高；纵轴表示竞争系数，参照所处的生态。右边这个图代表了两个物种竞争系数之间地关系，C，C'和C''三条直线代表三种不同的竞争关系，也就是说（这里暂时将种N认为是个固定的值），具体含义参照L-V模型或者本文的方程（1）。那么右图中，直线C越靠近原点，代表竞争越小，之间的关系Q相切并且在P-Q曲线内测的C表示两个物种刚好有一点生态位充电，存在最小的竞争；而P就代表了最激烈的竞争。因此，为了避免竞争，P会向右移动，则其表型的相似性也就拉开了。图3和图2类似，只是其两个物种表型相似度更高，理论上讲生态位也更加相似。

现在假定有一个外来的物种进入了原有的这个群落，其生态位正好是在两个物种之间，那么，如果进来的物种与直线C正切的地方是个负数，即，那么新来的这个物种就会被撵出去，反之则会成功的入侵。对于图2的情况，外来的物种的表型会向原来两个物种的种间位置移动，而对于图3的情况，外来的物种则会朝着二者中的某一种的表型靠近。